There are many knitting programs that will perform the necessary calculations, as well as a variety of knit calculators. The diophantine formula is the basis for what is known to some knitters as the “magic formula”. In the early 1980s, Alles Hutchinson authored a small book on the subject. There is a bit of personal leeway in the results, and the formula may be used in calculating even complex shapes with the proviso that one has the patience to break such shapes into series of simpler ones.
There are many online resources for information and calculators to sort out the math, including a triangle calculator. The original website’s offerings are now closed, but the info remains available here
https://web.archive.org/web/20200224005535/http://www.getknitting.com/ak_0603triangle.aspx
Using the gauge to match the previous post of 4S and 6R per inch the calculation for the pie divided into five triangles breaks down into the web calculator result pictured below:
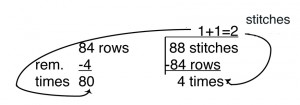
 The longhand method for the same calculation follows and also translates to: bring into hold 2 stitches for 4 times, 1 stitch for 80 times. Stitches in shaping are proofed as above: 88 stitches shaped over 84 rows.
The longhand method for the same calculation follows and also translates to: bring into hold 2 stitches for 4 times, 1 stitch for 80 times. Stitches in shaping are proofed as above: 88 stitches shaped over 84 rows.